The Quantum Superposition Explained Conceptually
The Qubit Is Not Like A Classical Bit - Not Even Conceptually
Don't waste your time with incomprehensible descriptions of the quantum superposition. If you only use quantum systems as a tool, you can safely skip the math. All you need to learn is how to turn the quantum knobs and handles to produce a quantum state vector that represents the problem at hand we aim to solve.

The internal state of a qubit - the quantum superposition - determines the probability of measuring the qubit as either or . However, explaining the quantum superposition in an understandable way seems to be a tricky endeavor. Thus, there are anecdotal descriptions in popular culture that range from inaccurate to outright false and misleading.
Take Schrödinger's cat, for example. It is the most iconic way to explain the strange and counterintuitive nature of quantum mechanics. But if someone told me about a cat that was alive and dead at the same time, I would think of an undead cat with scraps of fur hanging from it as it slowly rots away.

The Story Of Schrödinger's Cat
Schrödinger's cat is a famous thought experiment in quantum mechanics proposed by physicist Erwin Schrödinger in 1935.
Schrödinger envisioned a scenario in which a cat is placed in a sealed box along with a vial of poison and a radioactive source. The box also contains a mechanism that releases the poison and kills the cat when it detects the radioactive decay.
According to quantum mechanics, the radioactive source exists in a superposition of decayed and undecayed states until it is observed. Schrödinger extended this concept to the macroscopic level and proposed that the cat is simultaneously alive and dead until someone opens the box to observe its state.
Schrödinger's cat makes it clear how counterintuitive the world of quantum mechanics is. But it doesn't help us understand quantum superposition or even learn how to use quantum algorithms to solve real-world problems.
Don't waste your time on incomprehensible descriptions of the quantum superposition.
Unfortunately, unless you have a penchant for math terms and equations, the scientific community's explanations aren't much better.
Take a look at the following explanation.
The superposition of a two-dimensional quantum system (such as a qubit) is a complex (as in complex numbers) linear combination of its mutually orthogonal basis state vectors ( and ): where is the complex scalar amplitude of measuring , and the amplitude of measuring the value .
If you are already familiar with the quantum superposition, you will recognize a certain beauty in this explanation. It is as short as it is precise.
But almost every single word in this explanation brings with it a whole topic in itself, which, if you don't already know it, needs further explanation.
So all we have is a very good explanation for those who know quantum superposition already.
But what about those who don't?
Honestly, what's the point of an explanation if it's only for those who no longer need it because they already know what's going on?
If you are not familiar with the quantum superposition, this description is probably all Greek to you.
Speaking of Greek: dealing with quantum superposition is just as challenging as Icarus trying to cross the sea. If you fly too close to the sun, it will melt the wax on your wings. If you fly too low, the humidity of the sea will do the rest and cause you to crash.

If we remain too general, we are left with completely unwarranted assertions. For example, why does the internal state of the qubit determine the probabilities and not the actual observed values?
Although everyone in the quantum computing community accepts that quantum systems are inherently probabilistic, I have yet to find a reasonable explanation for this.
But if you don't even delve very deeply into these kinds of topics, all you get is a whole encyclopedia crammed with physics jargon and mathematical equations that not even the brightest students understand.
What we really need is an explanation that is not too superficial or too complex, but one that serves those who are unfamiliar with the concept of quantum superposition. One that gives a conceptual explanation that is rooted in physics, but only uses math where we need it to either understand what is going on, or where the math is the knob we have to work with.
“But perhaps the whole idea of quantum mechanics is too complex and counterintuitive to be explained conceptually without math,” you say?
“Maybe there's just no one who understands it well enough to explain it to a child.”
In a discussion with de Broglie on the platform of the Gare du Nord in Paris, whence they had traveled from Brussels to attend the Fresnel centenary celebrations, Einstein once said
that all physical theories, their mathematical expressions apart ought to lend themselves to so simple a description "that even a child could understand them.
And, by the way, didn't Icarus crash?
These are all legitimate objections. But I cannot accept that explaining the quantum superposition should not be possible.
Ultimately, we are not interested in understanding quantum mechanics or its nature. We want to shed just enough light on quantum systems to understand the practical implications of using them as a tool.
We do this by treating a quantum system as a probabilistic model and a qubit as a binary random variable.
In this context, the quantum superposition plays the role of the parameter , which determines the probabilities of measuring the qubit as or.
Remember that as someone who wants to develop quantum algorithms, you are using a quantum computer. Therefore, you don't need to understand how quantum systems work physically, but how to use them as a tool.
Essentially, we want to understand two things.
- Why can't we use a simple floating point number to describe the probability?
- What do we need to use instead?
What is the quantum state and how does this determine the probability that a qubit is measured as either 0 or 1?
The quantum state is inextricably linked to the wave-like properties of the subatomic particles.
Inspired by Einstein's work on the wave-particle duality of light, the French physicist Louis de Broglie proposed in 1924 that particles could have wave-like properties. This idea was revolutionary at the time. Louis de Broglie was awarded the Nobel Prize in Physics in 1929 for his discovery of the wave-like nature of electrons .

The basic properties of waves that interest us most in quantum mechanics are the wavelength, amplitude and phase.
The wavelength is the distance between two consecutive wave crests or troughs. It is usually denoted by the Greek letter lambda (λ) and measured in units of length, e.g. meters. The wavelength is inversely proportional to the frequency, i.e. if the wavelength increases, the frequency decreases and vice versa.
The amplitude is the maximum displacement of a wave from its rest position. It represents the height of a wave crest or the depth of a wave trough, measured from the center of the wave. The amplitude is directly related to the energy transported by the wave - the higher the amplitude, the more energy the wave contains.
The phase describes the position of a wave at a certain point in time relative to its starting point or another reference wave. It can be thought of as the "current state" of the wave in its motion cycle. The phase is particularly important when comparing two or more waves, as it determines how they interact with each other.
In addition to these properties of a single wave, the most important property of waves is their ability to interact. When waves overlap, they form compound waves.
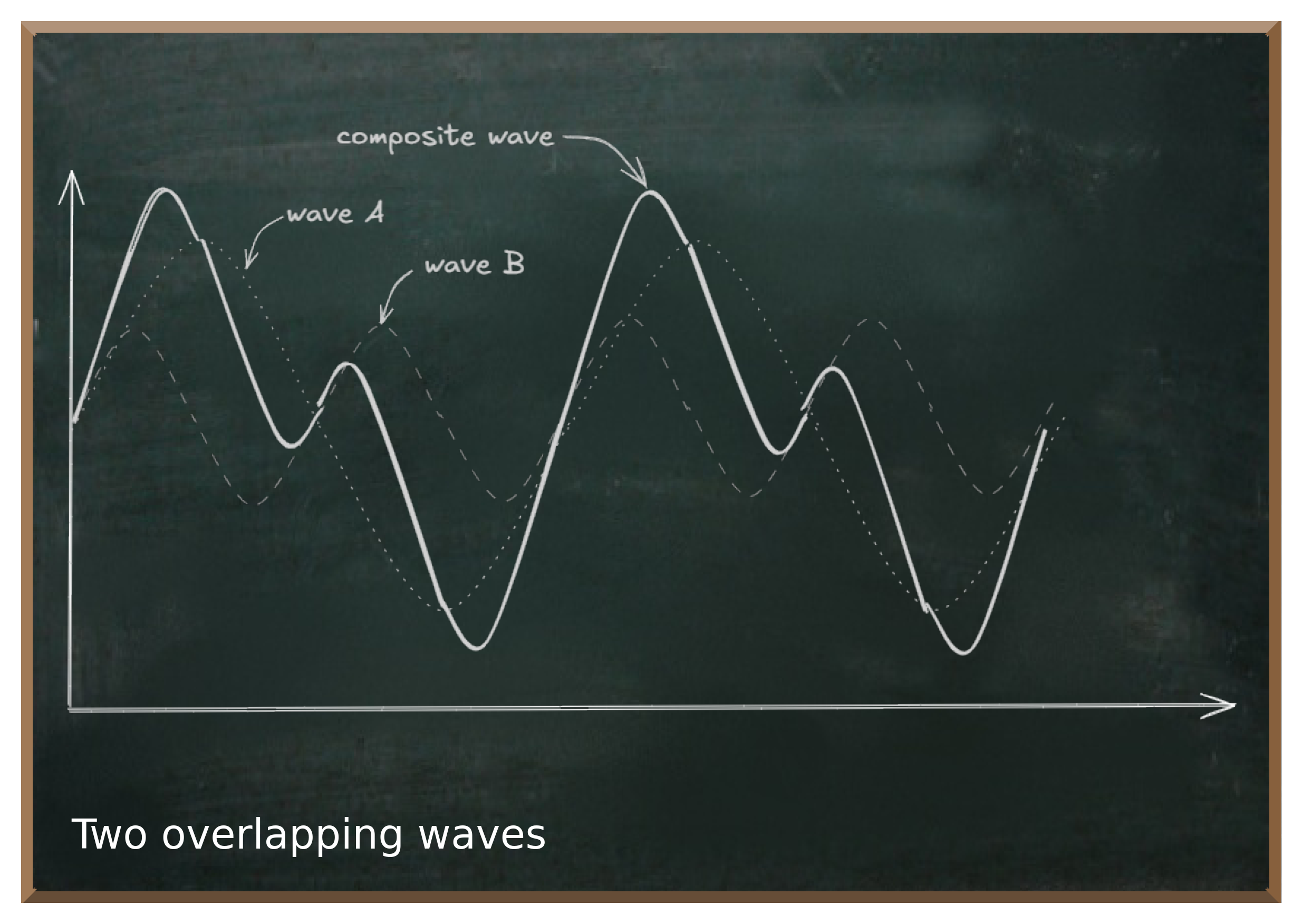
This property is the secret ingredient that turns subatomic particles into probabilistic systems and thus into an invaluable tool for solving problems.
The qubit is a bipartite quantum system. This means that it is made up of two waves with different wavelengths. The wavelength is the distinguishing feature that allows us to recognize the difference between the two waves. Each of these waves corresponds to one of the two possible outcomes - the basis states - which we commonly interpret as and .
Each of the two waves has a certain amplitude. As waves with larger amplitudes carry more energy, they are more likely to be detected - especially if they overlap with other waves.
Just think of the sea. The higher a wave is, the easier it is to see.
The greater the amplitude of the wave of a base state, the more likely we are to see it. And this also applies to a qubit. The probability of measuring a qubit as one of its base states corresponds directly to the amplitudes of the waves of the basis states.
Even although their amplitudes are properties of the individual waves of the basis states, they are not independent of each other.
But the amplitudes of the two basis state waves are normalized so that the sum of their absolute squares is equal to .
In simple terms, this means: The greater the amplitude of one basic state wave, the smaller the other.
To illustrate this concept, let's consider a sphere that we divide into two hemispheres. Each hemisphere of the sphere corresponds to one of the base states. The northern hemisphere corresponds to the basis state wave, which we interpret as , and the southern hemisphere to the one we interpret as .

If we look at this hemisphere from the equator, we see the same amount of both hemispheres. Both amplitudes are the same size.
However, the closer we get to the north pole, the more we see the northern hemisphere and less the southern hemisphere. So while the amplitude of the northern basis state increases, the amplitude of the southern basis state decreases.

If we look at the sphere from the north pole, we only see the northern hemisphere. Although the wave representing the southern hemisphere still exists, we can no longer see it because its amplitude is .
In this example, the perspective we apply to a quantum system determines how much we see of each of its basis states.
So, how do we describe this perspective onto this sphere?
The most convenient way is a vector that originates at the center of the sphere and points to the point at the surface from where we look at the
A vector is a geometric object. We can imagine a vector as a directed line segment that has a magnitude (length) and a direction (from the tail to the head, indicated by an arrow).
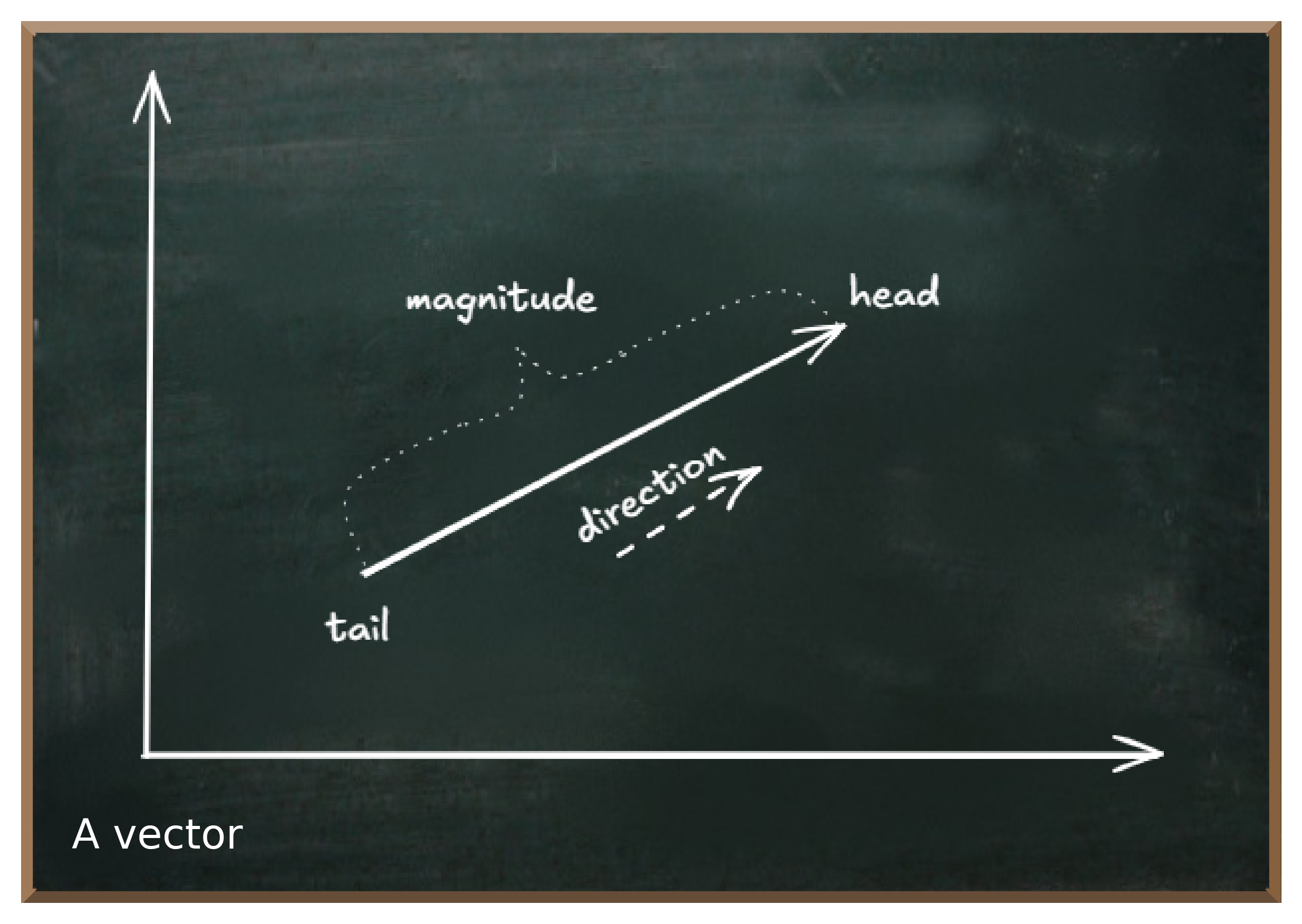
So the quantum state vector has its origin in the center of the sphere and points to somewhere on the surface. This point is the perspective from which we view the sphere and therefore determines how much of both hemispheres we "see".
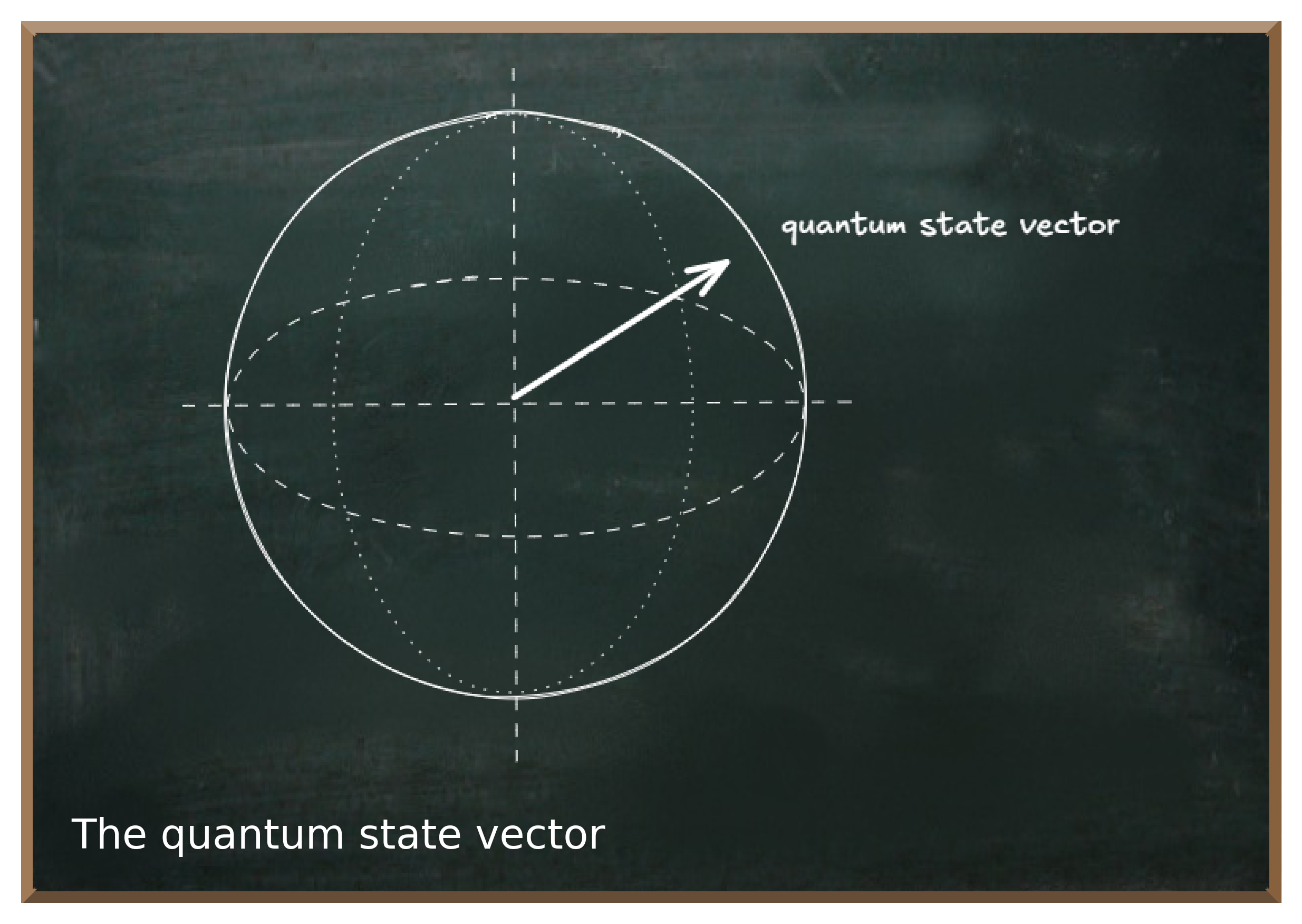
Even though we don't want to be mathematicians or physicists, it's important to understand the key terms and concepts you'll come across when reading about quantum computing. But don't worry, we'll only go into the essentials and leave out all the superfluous details.
Mathematicians usually write vectors vertically, like a matrix with a column in which each number corresponds to a dimension of the vector.
However, quantum physicists commonly represent column vectors by the "ket" construct of Dirac notation, which looks like this: . This is the quantum state vector that we usually call “psi” (). So whenever you see anywhere, you can be pretty sure that the author means a quantum state vector.
is a two-dimensional column vector, where the first (upper) dimension corresponds to the amplitude () of the basis state wave that we interpret as 0 and the second (lower) dimension corresponds to the amplitude () of basis state wave that we interpret as 1.
Another way of writing this quantum state vector is as the sum of its basis states. That is
Due to the normalization mentioned above, which states that one dimension must decrease if the other increases, there are two special cases. If one amplitude becomes , the other inevitably becomes and vice versa.
- (called "ket zero") is a vector that points to the north pole and therefore, we only "see" the basis state wave that we interpret as .
- (called "ket zero") is a vector that points to the south pole therefore, we only "see" the basis state wave that we interpret as .
Thus far, I have always referred to the basis state waves, which we interpret as either or . But in short, we use and as names for the two basis states of a qubit.
For the sake of simplicity, we assume a two-dimensional representation of the sphere - a circle in which the top of the circle corresponds to the basis state and the bottom to the basis state .
The following figure illustrates this simplified representation of the two basis states and an arbitrary quantum state vector .
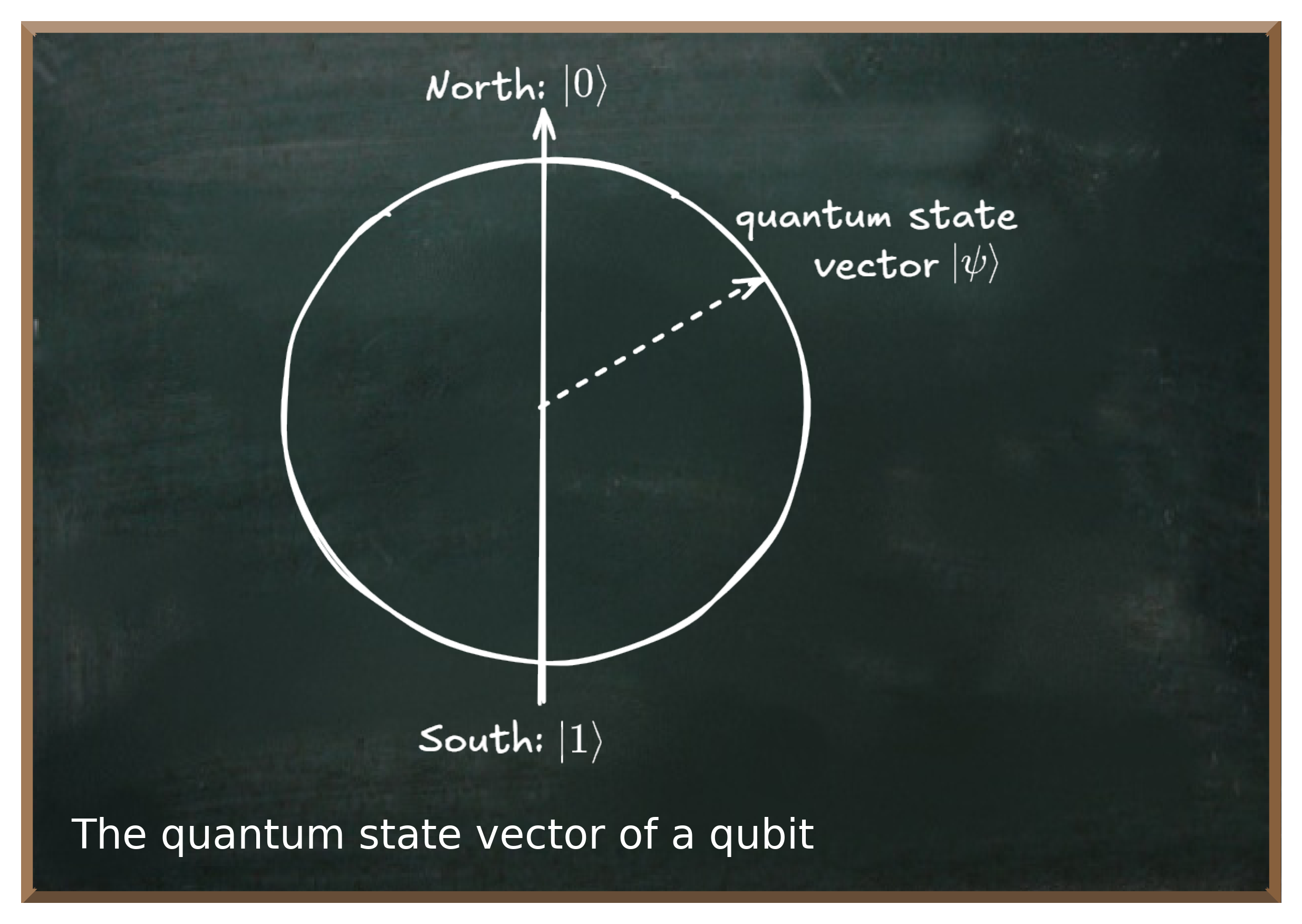
This representation differs from other two-dimensional representations in that both dimensions (the basis states and ) reside on the vertical axis.
With two dimensions, it is usual to set the two dimensions orthogonally to each other. This means that one axis points upwards and the other to the right.
In a qubit, however, the two basis states and are not only orthogonal to each other, but are also mutually exclusive due to normalization. In other words, the more the qubit is in the state the less it is in the state. In addition, the arrangement of and on opposite poles of the vertical axis enables an intuitive representation of superposition states that point to any point on the circular surface.
The distances between the head of the quantum state vector and the opposite pole correspond to the amplitude of a basis state.
And finally, the probability of measuring the qubit as either basis state equals the absolute square of the corresponding amplitude:
For example, - the closer this point is to the north pole, - the greater the distance to the south pole, - the greater the amplitude of the state, - the more we “see” of the northern hemisphere (or the semicircle), - and the more likely we are to observe the qubit in the basis state we interpret as .
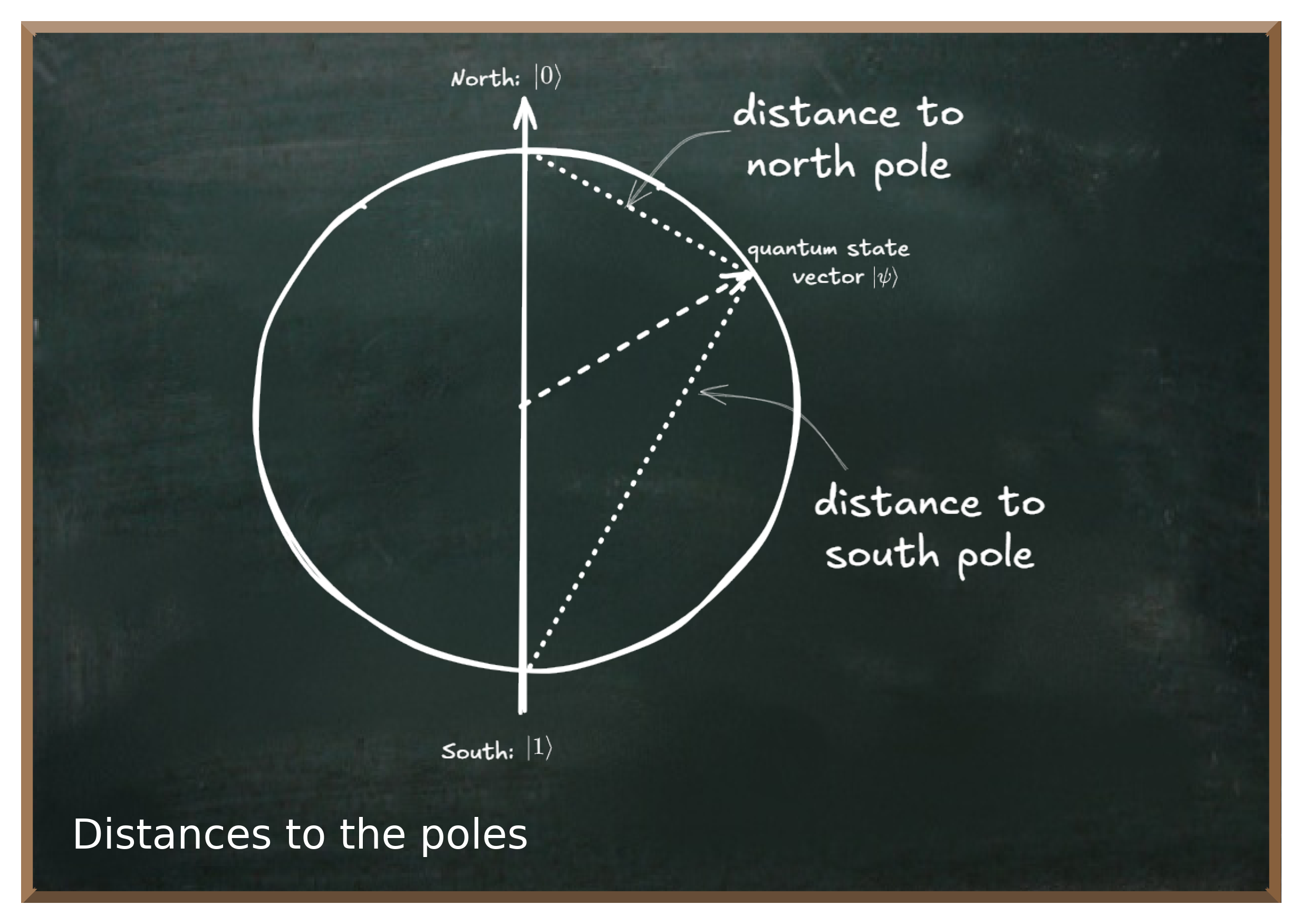
The quantum state vector is therefore the key feature that corresponds directly to the probabilities of measuring the qubit as either or .
This raises the intricate question of what we actually get when we measure a qubit.
Can't we just examine the wavelengths, amplitudes and phases of the waves to gather all the information that the quantum system contains?
The short answer is: “No, we can't!” We cannot simply look at the entire composite wave and reveal all of its features.
Ultimately, we are talking about particles on a subatomic level. In order to obtain information from such a tiny system, we need a measuring device that interacts with it and returns information about it.
The quantum system could be a photon, for example, and the device we use to measure it is a photodetector that absorbs photons to generate a current pulse. This allows us to see the position of a photon, but once we see it, there is no photon left behind. By converting it into a current pulse, we effectively destroy it.
And the fate of a qubit is not much better as soon as we measure it. We destroy its state of being composed of two basis states. When we interact with a quantum system, it collapses into the wave of one of its two basis states or . Nothing remains of the wave of the other basis state, and we lose a lot of information, such as the amplitudes of the original state waves that characterize the quantum state vector.
An important question is, of course, into which of the two basis states does the composite wave collapse? In our visual example of the sphere, we said that we see more or less of the two hemispheres depending on the perspective described by the quantum state vector. This means that the more we see of one of the hemispheres, the more likely it is that the total wave will collapse into this basis state.
For instance, if we look at a qubit in the state, we are looking at it from the north pole. Consequently, we only see the northern hemisphere, which corresponds to the value . Then there is a probability of that the qubit will collapse into the state it was already in.
However, if the qubit is in any quantum state that is not or , for example in a state in which both basis states are equally likely (from the equator), then the pure act of interacting with the qubit collapses this state into one of the two basis states.
Suppose we look at the qubit from the perspective of its equator. Then the amplitudes of both base states are the same and the probability of measuring the qubit as either or is also the same. That is in each case. But as soon as we measure the qubit, we collapse its state.
For example, let's assume it collapses in . Consequently, our device only measures the wavelength corresponding to and we interpret the measurement as . But we have no idea of the amplitudes of the waves before the measurement. And if we were to measure the qubit again, we would now get each time, because the quantum state has collapsed into the state , which we let collapse into again and again.
However, if a qubit is neither in the state nor in the state, but in a composite quantum state , then we do not know which one it will collapse into. That is random. And by random, we mean truly random.
According to Heisenberg's uncertainty principle, the accuracy with which physical properties of a particle can be determined simultaneously is limited. And at the extremely tiny level of atoms and subatomic particles, these limits become significant.
The more precisely we determine the wavelength of the qubit - which we must do in order to interpret the measurement as either or - the less we can learn about its amplitude - or even about the quantum state vector itself. So even if there were an underlying factor that determined which of the two base states the composite wave collapses into, we would never be able to find out.

Therefore, most of the information that the quantum state contains remains hidden to us.
The best we can do is to take samples. We repeatedly prepare the quantum systems with the same quantum state and measure them. In the end, we obtain a probability that corresponds to the squared amplitudes of the base states.
The quantum state vector determines the probability of measuring a qubit in a certain basis state, yet which of both is random within the limits of the amplitudes of the basis state waves that determine these probabilities.
Even though working with a vector is a little more complicated than with a simple floating point number, it does not require a degree in math. Fortunately, in fact, we have computers (both classic and quantum) to do the math for us.
All we need to learn is how to turn the quantum knobs and handles to produce a quantum state vector that represents the problem at hand we aim to solve.