The Best Explanation Of Quantum Systems To Start With
Proceed to other explanations afterward
Understand quantum systems from a perspective that helps you use them as a tool to solve practical problems. "Otherwise you could be smashed against the overhanging rocks, against which the deep blue waves of the Amphitrite beat with terrific fury."

Starting to learn about quantum systems is as dangerous as Odysseus' attempt to pass by the Sirens. Just like the Sirens, quantum systems first enchant all who come near them. It is too tempting to start studying quantum systems from the physicists' perspective.
If any one unwarily draws into close and hears the singing of the Sirens, his wife and children will never welcome him home again, for they sit in a green field and warble him to death with the sweetness of their song.
It is the path paved by Nobel prize winners. You will be following in the footsteps of Albert Einstein, Erwin Schrödinger, Paul Dirac, Werner Heisenberg, Niels Bohr, Richard Feynman (not in this picture), and many more.

At the famous Solvay Conference on Physics (1927), the world's most important physicists met to discuss the newly formulated quantum theory. 17 of the 29 participants were awarded the Nobel Prize.
At first, the beautiful explanations of quantum mechanical concepts will cast a spell over you.
- Quantum Superposition: A particle exists in multiple states at the same time.
- Quantum Entanglement: Two particles sharing a state, no matter how far apart they are in the universe.
- Quantum Randomness: Only when you measure a quantum system does it randomly take on a definite state.
But they show their ghastly faces as soon as you go into more detail.

Suddenly, you cope with these things:
- The superposition of a two-dimensional quantum system (such as a qubit) is a complex (as in complex numbers) linear combination of its mutually orthogonal basis state vectors ( and ):where is the complex scalar amplitude of measuring , and the amplitude of measuring the value .
- In an entangled bipartite quantum system composed of two particles, and , the joint wave function of the system cannot be written as a simple product of the wave functions of each particle, such as . Instead, it might take a form like, where the coefficients reflect the correlations between the states of particles and .
- The projective measurement outputs outcome with probability and leaves the system in the renormalized state . This measurement projects the input state into one of the orthogonal subspaces corresponding to the projection operators , with probability equal to the square of the size of the amplitude of the component of in that subspace.
The problem is that the existing explanations of quantum systems are aimed at budding aspiring physicists who want to understand what is physically going on there. But these explanations do not help to develop algorithms that solve real problems.
Just like the sorceress Circe who warned Odysseus of the danger he was about to face, I caution you not to begin your quantum computing journey the physicist's way.
As someone who aims to develop quantum algorithms, you are someone who uses a quantum computer. Therefore, you need to understand how to perform meaningful computations.
And that requires a very different view of quantum systems than the quantum mechanical perspective can provide.
Of course, I know quantum physics is the way all students start learning quantum computing.
Of course, I know all other textbooks, and courses use this perspective to teach quantum computing.
But, of course, I also know that this way is excruciating.
In fact, the implications of quantum mechanics are not immediately straightforward to the computational
There is a great heap of shattered students lying all around, with started textbooks, unread scientific papers, and myriads of web bookmarks rotting off.

So, if even physics students, who obviously have a penchant for studying theoretical constructs using mathematical formulas, have a motivation problem to master the subject, how will you fare?
The perspective you take when conceptualizing quantum systems is key to your understanding.
So, choose wisely!

I would like to give you an alternative explanation for quantum systems. One that does not involve physics and complicated equations. But one that fosters understanding quantum systems and depicts clear practical implications.
This is the perspective of a quantum system as a probabilistic model.
A probabilistic model uses probability distributions, conditional probabilities and randomness to reason about uncertain events and make predictions.
This perspective teaches us a lot about the usefulness of a quantum system for computation. Not only does it provide a clear description of what we can use a quantum system for
- to reason about uncertain events and make predictions
- but it also helps to identify the relevant knobs and handles to know when using a quantum system as a computational tool
- probability distributions, conditional probabilities and randomness.
If we look at a quantum system as a probabilistic model, we can suddenly get a lot more out of quantum superposition, entanglement and randomness than if we just read the superficial popular press or the rigorous mathematical papers.
For instance:
- The quantum superposition is nothing more than the physical mechanism that allows us to use marginal probability distributionsto represent the uncertainty and variability of the variables of our model.
- Quantum entanglement is nothing other than the physical mechanism that allows us to capture dependencies and interactions between variables.
- And the inherent quantum randomness is nothing more than abuilt-in, bias-free sampling algorithm that we can use to deal with the probabilistic nature of real events.
Of course I can hear all the hypsters scream. And, all the serious physicists will criticize such a perspective as too simplicistic. But it is the one perspective you start with. Not the last thing you'll ever hear or read about the quantum superposition, entanglement, and randomness. In fact, the very next posts in this module shed much more light on these topics.
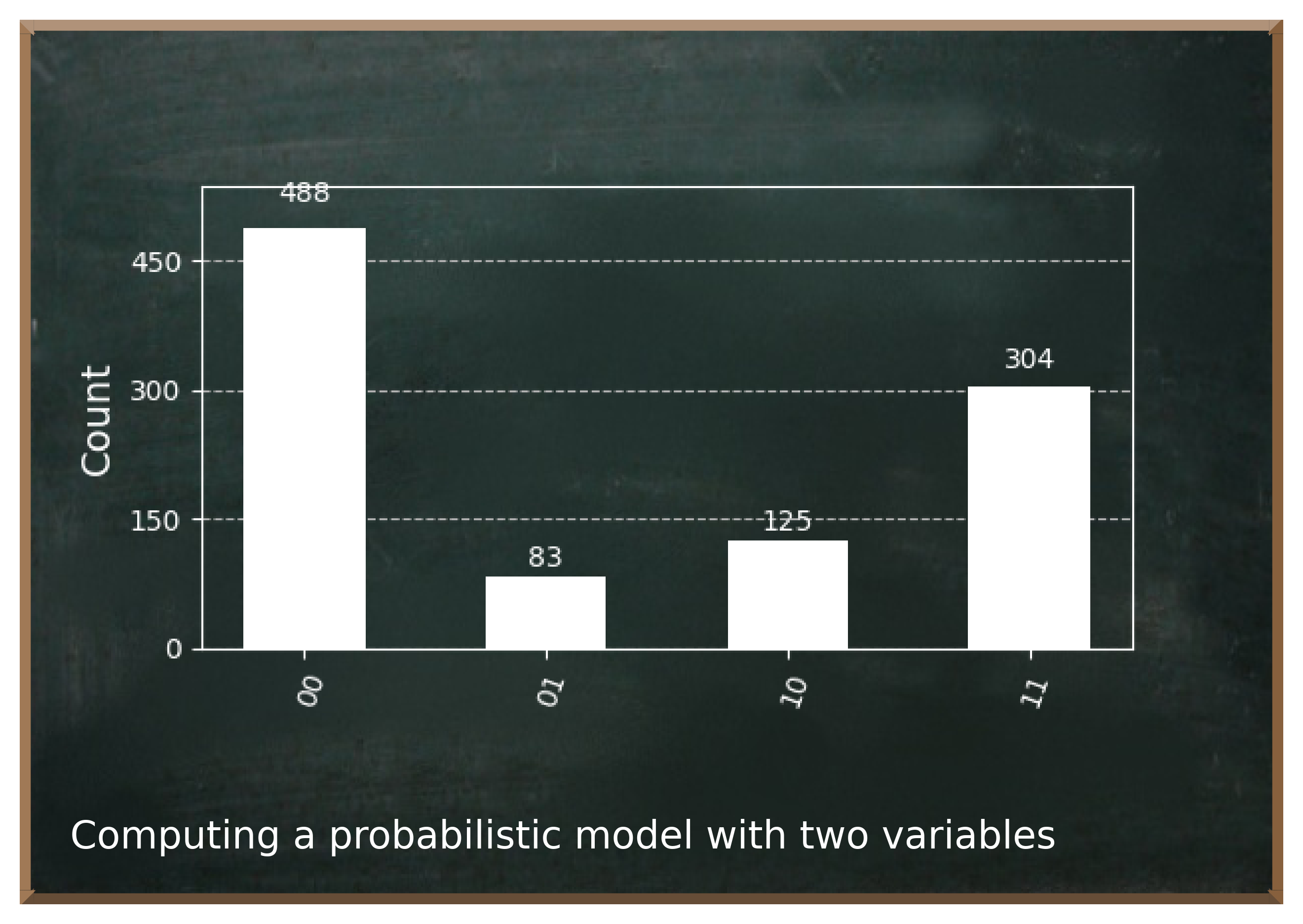
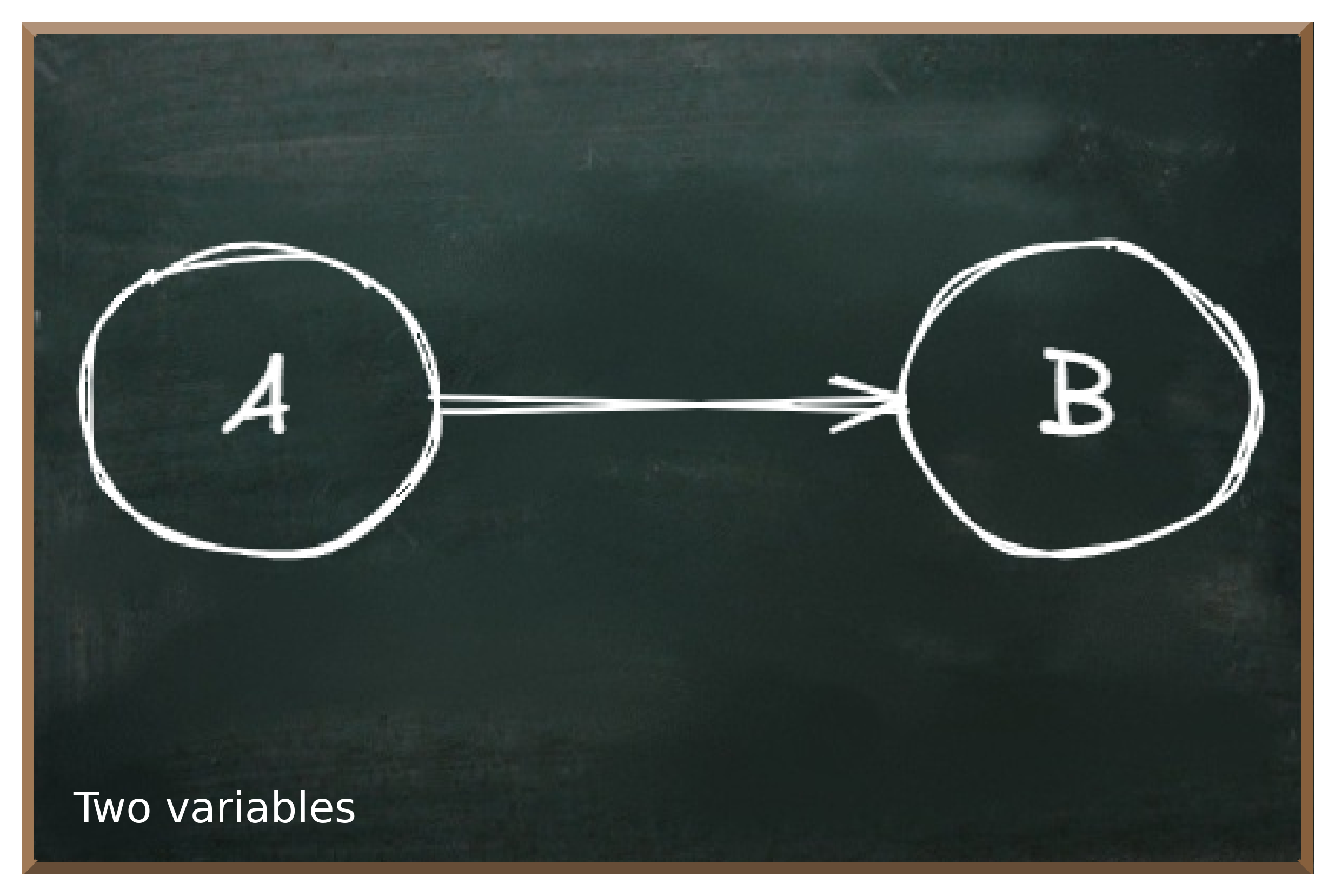
But rather than bore you with a long theoretical essay, let me demonstrate right now - with code - how we use a quantum system to represent and reason about a small probability model like the one in the figure below with two binary variables and .
is an explanatory (independent, predictive) variable that can take on any valid value ( or , because it is binary). But we don't know much about that yet.
, on the other hand, is a response (dependent, outcome) variable. It can also be anything ( or ). But we know that its value somehow depends on the value of . Therefore, explains the variations of .
So let's be more precise and say that the variable takes the value with a probability of . Furthermore, the variable only takes the value with a probability of only if the variable is .
We start with the declaration of a QuantumCircuit with two qubits. A quantum circuit is a model for a quantum computation that represents the sequence of operations applied to qubits over time.
With the results obtained from running this model, we can now analyze other probabilities that we did not explicitly specify in our model, such as the overall (marginal) probability of measuring the variable as . This is the sum of all states in which the lower left qubit is . Since we only have one of these states (), the marginal probability that the variable is corresponds to the probability of this state: .