What the CNOT Operator Really is

Unlearn your belief in causality, you must

You've been misled about the CNOT gate. Open almost any textbook and you'll read: “If the control qubit is |1⟩, flip the target.” But CNOT is not a cause-and-effect gate. Let's take a look at what it is instead.

by Frank Zickert

October 02, 2025

You've been misled about the Controlled Not Gate.A controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate That neat line you've seen in textbooks, If the control qubit is is a basis state.
Learn more about , flip the target., isn't just oversimplified. It's a trap.

Hold on to that picture and you'll confuse the Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate with copying, mistake symmetry for causality, and completely miss why this Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate is the beating heart of Quantum Algorithms.A quantum algorithm is a step-by-step computational procedure designed to run on a quantum computer, exploiting quantum phenomena such as superposition, entanglement, and interference to solve certain problems more efficiently than classical algorithms.
Learn more about Quantum Algorithm You'll be stuck thinking in classicalif–then–else code, while the quantum story passes you by.

The Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate isn't a cause-and-effect Quantum Gate.A quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate Let's take a look at what it is instead.

This post is accompanied by a PDF file summarizing the key points.

Please Login to Download the PDF (your PyQML subscription works here!)

Textbook explanations peddle the illusion of causality. Let's grab THE standard textbook on quantum computation: Nielsen and Chuang (2010).

‘If A is true, then do B’. This type of controlled operation is one of the most useful in computing, both classical and quantum.
—Nielsen, M.A.Quantum computation and quantum information

How about this one:

The controlled-not gate, Cnot, acts on the standard basis for a two-qubit system, with is a basis state.
Learn more about and is a basis state.
Learn more about viewed as classical bits, as follows: it flips the second bit if the first bit is 1 and leaves it unchanged otherwise.
—Rieffel, E.Quantum computing: a gentle introduction

We could go on like this for quite a while. Another thing that almost every textbook does is provide a truth table as depicted in ? that maps inputs to outputs. I don't know, but if you put it that way, what do you think the Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate would be?

Figure 1 The truth table describing the effect of the CNOT when the control is in the computational basis

The Causal Mental Model Trap

The moment you describe the Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate as the control qubit flips the target, you've already stepped into a trap. It feels intuitive because it mirrors classical programming: if–then–else, cause and effect. But the Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate doesn't work like that. Treating it as causal has severe consequences:

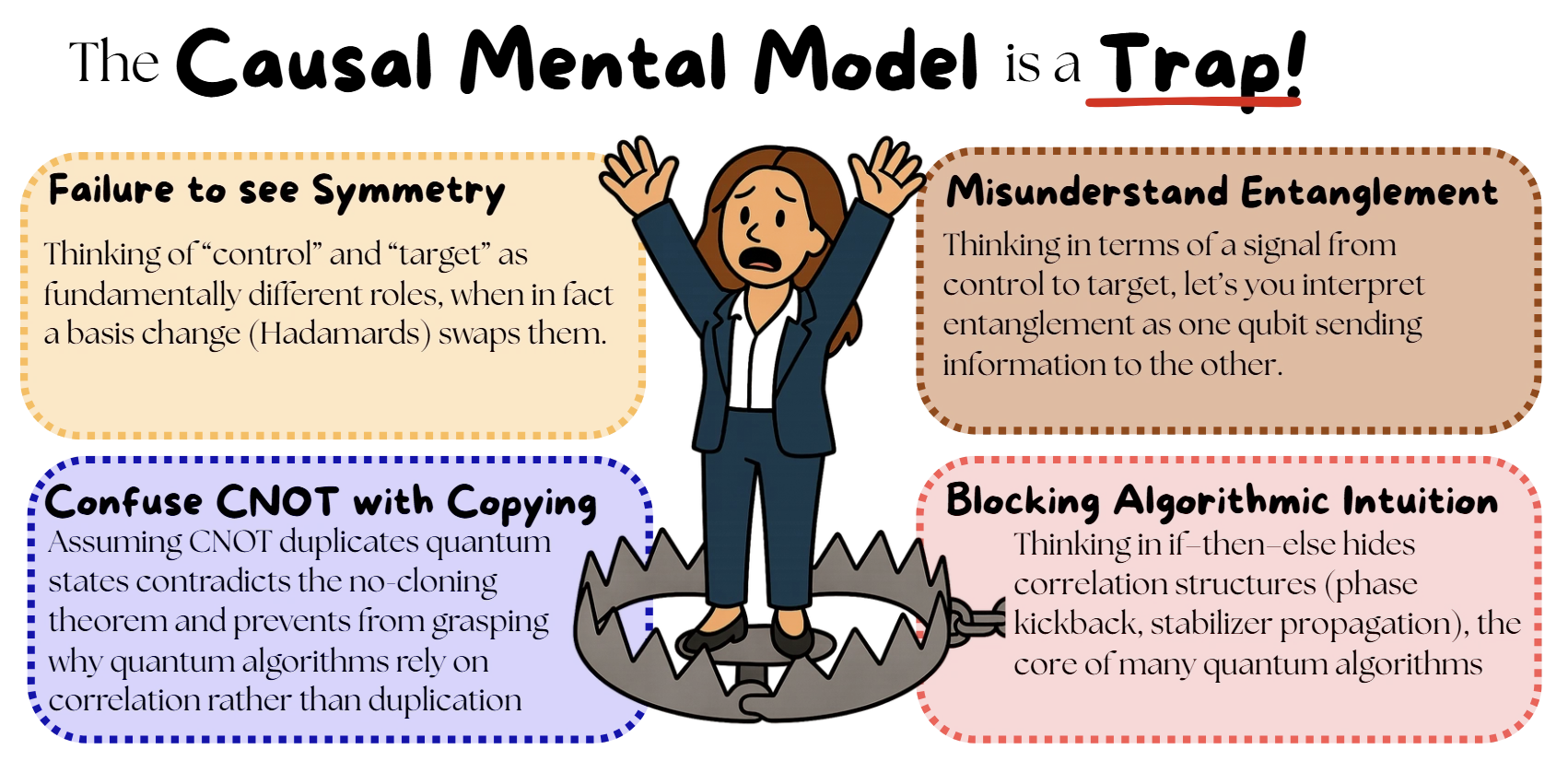
You confuse Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate with copying. Because only if the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in a Basis StateA basis state in quantum computing is one of the fundamental states that form the building blocks of a quantum system’s state space. For a single qubit, the basis states are and ; any other qubit state is a superposition of these. In systems with multiple qubits, basis states are all possible combinations of s and s (e.g., , , , and ), forming an orthonormal basis for the system’s Hilbert space.
Learn more about Basis State ( is a basis state.
Learn more about or is a basis state.
Learn more about ) and the target starts in is a basis state.
Learn more about , the Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate copies the control value to the target. But if the control is in a Superposition,Superposition in quantum computing means a quantum bit (qubit) can exist in multiple states (0 and 1) at the same time, rather than being limited to one like a classical bit. Mathematically, it’s a linear combination of basis states with complex probability amplitudes. This allows quantum computers to process many possible inputs simultaneously, enabling exponential speedups for certain problems.
Learn more about Superposition the result becomes an entangled pair and not two identical qubits. ).
You fail to see symmetry. The control target story makes one QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit sound like the active agent and the other like a passive receiver. In reality, nothing about the Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate is inherently directional. For instance, if the target is not state is a basis state.
Learn more about but in SuperpositionSuperposition in quantum computing means a quantum bit (qubit) can exist in multiple states (0 and 1) at the same time, rather than being limited to one like a classical bit. Mathematically, it’s a linear combination of basis states with complex probability amplitudes. This allows quantum computers to process many possible inputs simultaneously, enabling exponential speedups for certain problems.
Learn more about Superposition the Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate may not even affect the target but only the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (e.g. Phase KickbackPhase kickback is a quantum phenomenon where a phase shift applied to a *target* qubit in a controlled operation gets "kicked back" onto the *control* qubit instead. It happens because the control qubit’s superposition interacts with the target’s phase, effectively transferring that phase information to the control. This mechanism is fundamental in algorithms like phase estimation and the quantum Fourier transform.
Learn more about Phase Kickback).
You misunderstand EntanglementEntanglement is a quantum phenomenon where two or more particles become correlated so that measuring one instantly determines the state of the other, no matter how far apart they are. This correlation arises because their quantum states are linked as a single system, not as independent parts. It doesn’t allow faster-than-light communication but shows that quantum systems can share information in ways classical physics can’t explain.
Learn more about Entanglement. A causal picture makes it seem like one QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit sends information to the other, creating spooky action at a distance. That's a misconception. EntanglementEntanglement is a quantum phenomenon where two or more particles become correlated so that measuring one instantly determines the state of the other, no matter how far apart they are. This correlation arises because their quantum states are linked as a single system, not as independent parts. It doesn’t allow faster-than-light communication but shows that quantum systems can share information in ways classical physics can’t explain.
Learn more about Entanglement isn't messaging. It's correlation encoded by a joint Unitary Operator.A **unitary operator** is a linear operator ( U ) on a complex vector space that satisfies ( U^\dagger U = UU^\dagger = I ), meaning it preserves inner products. In simpler terms, it preserves the **length** and **angle** between vectors—so it represents a **reversible, norm-preserving transformation**. In quantum mechanics, unitary operators describe the evolution of isolated systems because they conserve probability.
Learn more about Unitary Operator Stick with causality, and you'll end up repeating the same tired faster than the speed of light-myths that Quantum MechanicsQuantum mechanics is the branch of physics that describes the behavior of matter and energy at atomic and subatomic scales.
Learn more about Quantum Mechanics has debunked for a century.

Not Faster Than The Speed Of Light

Coming soon...

You block algorithmic intuition. Quantum AlgorithmsA quantum algorithm is a step-by-step computational procedure designed to run on a quantum computer, exploiting quantum phenomena such as superposition, entanglement, and interference to solve certain problems more efficiently than classical algorithms.
Learn more about Quantum Algorithm use the Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate to build correlation structures, such as Phase Kickback,Phase kickback is a quantum phenomenon where a phase shift applied to a *target* qubit in a controlled operation gets "kicked back" onto the *control* qubit instead. It happens because the control qubit’s superposition interacts with the target’s phase, effectively transferring that phase information to the control. This mechanism is fundamental in algorithms like phase estimation and the quantum Fourier transform.
Learn more about Phase Kickback, Stabilizer Propagation,**Stabilizer propagation** is a method used in quantum computing to efficiently simulate how *stabilizer states* evolve under *Clifford operations*. Instead of tracking full quantum states, it tracks how the stabilizer generators (Pauli operators that define the state) transform through the circuit. This works because Clifford gates map Pauli operators to Pauli operators, keeping the stabilizer structure intact and making simulation polynomial-time efficient.
Learn more about Stabilizer Propagation Error-Syndrome Extraction.Error-syndrome extraction is the process in quantum error correction where measurements are used to detect which type of error (bit-flip, phase-flip, or both) has affected the encoded qubits, without collapsing their logical state. The outcome of these measurements—called the *syndrome*—indicates which correction operation is needed. Essentially, it identifies the error pattern while preserving the encoded quantum information.
Learn more about Error-Syndrome Extraction If you're stuck thinking in if–then–else terms, you'll miss that these aren't branches of execution but patterns of correlation. In other words, the causal model blinds you to the very mechanisms that give Quantum ComputingQuantum Computing is a different kind of computation that builds upon the phenomena of Quantum Mechanics.
Learn more about Quantum Computing its power.

Why CNOT is Not a Classical If–Then–Else

If you try to squeeze the Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate into the shape of a classical if–then–else statement, you immediately run into contradictions. The gate glitches under that interpretation:

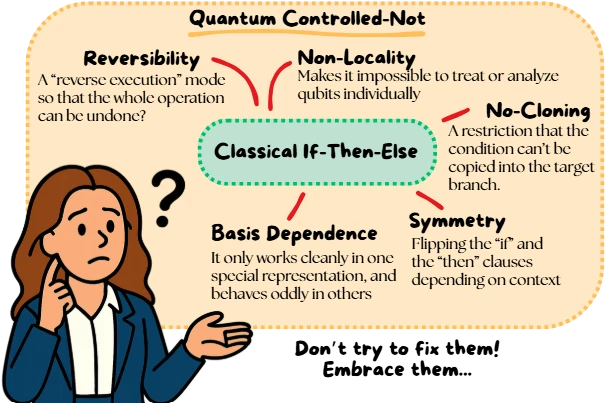
Listing 1 The CNOT is not a conditional statement with glitches

Reversibility: A classical branch discards information. Once you go down the then path, you can ignore the else path. The Controlled Not Gate,A controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate like all Quantum Gates,A quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate doesn't allow that. It is unitaryA **unitary operator** is a linear operator ( U ) on a complex vector space that satisfies ( U^\dagger U = UU^\dagger = I ), meaning it preserves inner products. In simpler terms, it preserves the **length** and **angle** between vectors—so it represents a **reversible, norm-preserving transformation**. In quantum mechanics, unitary operators describe the evolution of isolated systems because they conserve probability.
Learn more about Unitary Operator and therefore, must be reversible. So, you have to carry forward all the information about paths not taken.
No-Cloning Restriction: In classical control structures, the condition can be freely copied into different branches. In Quantum Computing,Quantum Computing is a different kind of computation that builds upon the phenomena of Quantum Mechanics.
Learn more about Quantum Computing the condition (usually a QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit in SuperpositionSuperposition in quantum computing means a quantum bit (qubit) can exist in multiple states (0 and 1) at the same time, rather than being limited to one like a classical bit. Mathematically, it’s a linear combination of basis states with complex probability amplitudes. This allows quantum computers to process many possible inputs simultaneously, enabling exponential speedups for certain problems.
Learn more about Superposition) cannot be cloned. The Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate respects this restriction. It doesn't copy theQuantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State of the control into the target. In fact, it doesn't copy any information at all. So, if you need any information twice, you have to prepare it twice. From the very begining.
Symmetry and Basis Dependence: The classical if–then–else has a fixed hierarchy: if first, then second. The Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate doesn't. Only in the Computational BasisThe computational basis is the standard set of basis states used to describe qubits in quantum computing. These are typically and for a single qubit. For multi-qubit systems all possible combinations of basis states denote the computational basis, like , , , and . These states correspond to classical bit strings and form an orthonormal basis for the system's Hilbert space. Any quantum state can be expressed as a superposition of these computational basis states.
Learn more about Computational Basis it looks like the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit controls the other, but apply a Hadamard OperatorThe Hadamard operator, often denoted H, is a single-qubit quantum gate that creates an equal superposition of and . In other words, It turns the states of the computational basis and into the states of the Fourier basis and .
Learn more about Hadamard Operator to the target and the roles swap. The very idea of a permanent controller and a passive target breaks down.
Non-Locality: Classical branches let you reason about variables independently. You know which path you're on. With Controlled Not Gates,A controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate you can't separate the QubitsA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit once they're entangledEntanglement is a quantum phenomenon where two or more particles become correlated so that measuring one instantly determines the state of the other, no matter how far apart they are. This correlation arises because their quantum states are linked as a single system, not as independent parts. It doesn’t allow faster-than-light communication but shows that quantum systems can share information in ways classical physics can’t explain.
Learn more about Entanglement. Their joint AmplitudesIn quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude are reshuffled, and you cannot treat them as isolated entities anymore.

These things aren't bugs to fix. They're the quantum features. The Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate isn't broken compared to classical control. It's showing you that the if–then–else model itself is the wrong metaphor.

What the CNOT Actually Is

Join to continue

This part is available to PyQML students and above. Log in or start a subscription to unlock member content.

Already a member? Use Log in. New here? Choose Subscribe.

The mathematician will give you the most precise definition: the unitary matrixA **unitary operator** is a linear operator ( U ) on a complex vector space that satisfies ( U^\dagger U = UU^\dagger = I ), meaning it preserves inner products. In simpler terms, it preserves the **length** and **angle** between vectors—so it represents a **reversible, norm-preserving transformation**. In quantum mechanics, unitary operators describe the evolution of isolated systems because they conserve probability.
Learn more about Unitary Operator depicted in ?. Unfortunately, this is also the least intuitive, unless you multiply matrices and vectors in your dreams.

Figure 2 The matrix of the CNOT operator

Much more intuitive is the image of the Quantum CircuitA quantum circuit is a sequence of quantum gates applied to qubits, representing the operations in a quantum computation. Each gate changes the qubits’ state using quantum mechanics principles like superposition and entanglement. The final qubit states, when measured, yield the circuit’s computational result probabilistically.
Learn more about Quantum Circuit shown in ? or the source code provided in ? .

Figure 3 The quantum circuit representation of the CNOT gate

bell-state.py

from qiskit import QuantumCircuit

# quantum circuit with two qubits

qc = QuantumCircuit(2)

# CNOT with control=0, target=1

qc.cx(0, 1)

Listing 2 How to use the CNOT in Qiskit

Although these illustrations clearly show which qubit acts as the control and which acts as the target, they do not reveal anything about their effects.

So, let's strip away the metaphors and CNOT becomes simple. It is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit operatorA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate that swaps Amplitudes.In quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude You can write any two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State as with (in this case) the left digit inside the kets is the control qubit and the right digit is the target; are the complexA complex number is a number that has two parts: a real part and an imaginary part, written as , where . The real part behaves like ordinary numbers, while the imaginary part represents a direction perpendicular to the real axis on the complex plane. Complex numbers let us represent and calculate quantities involving square roots of negative numbers.
Learn more about Complex Number AmplitudesIn quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude of the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit ; and are the complexA complex number is a number that has two parts: a real part and an imaginary part, written as , where . The real part behaves like ordinary numbers, while the imaginary part represents a direction perpendicular to the real axis on the complex plane. Complex numbers let us represent and calculate quantities involving square roots of negative numbers.
Learn more about Complex Number AmplitudesIn quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude of the target QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit

The following ? shows the effect of the Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate on these two qubits.

Figure 4 Effect of the CNOT operator

The Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate has a very simple effect. It swaps the AmplitudesIn quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude of and . That's it.

No signals, no hidden messages, no causal arrows. Just a reshuffling of Amplitudes.In quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude A few things immediately follow:

No information is gained or lost.
The operation is unitaryA **unitary operator** is a linear operator ( U ) on a complex vector space that satisfies ( U^\dagger U = UU^\dagger = I ), meaning it preserves inner products. In simpler terms, it preserves the **length** and **angle** between vectors—so it represents a **reversible, norm-preserving transformation**. In quantum mechanics, unitary operators describe the evolution of isolated systems because they conserve probability.
Learn more about Unitary Operator, so the four AmplitudesIn quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude are simply rearranged.
No copy is made. The copy illusion only holds for trivial Basis States,A basis state in quantum computing is one of the fundamental states that form the building blocks of a quantum system’s state space. For a single qubit, the basis states are and ; any other qubit state is a superposition of these. In systems with multiple qubits, basis states are all possible combinations of s and s (e.g., , , , and ), forming an orthonormal basis for the system’s Hilbert space.
Learn more about Basis State and vanishes as soon as the control is in SuperpositionSuperposition in quantum computing means a quantum bit (qubit) can exist in multiple states (0 and 1) at the same time, rather than being limited to one like a classical bit. Mathematically, it’s a linear combination of basis states with complex probability amplitudes. This allows quantum computers to process many possible inputs simultaneously, enabling exponential speedups for certain problems.
Learn more about Superposition.
No directionality exists. The so-called control and target are labels of convenience. Apply Hadamard OperatorsThe Hadamard operator, often denoted H, is a single-qubit quantum gate that creates an equal superposition of and . In other words, It turns the states of the computational basis and into the states of the Fourier basis and .
Learn more about Hadamard Operator to the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit and their roles swap.
No causation is implied. The whole operation applies jointly; it doesn't matter which wire is drawn on top.

Think of the Controlled Not GateA controlled-NOT (CNOT) gate is a two-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate where the first QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (control) determines whether the second QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit (target) is flipped on the -axis. If the control QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state is a basis state.
Learn more about , the target Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is inverted . If the control is is a basis state.
Learn more about , the target is unchanged. It’s essential for creating entanglement, since applying aCNOT to a superposed control qubit links the states of both qubits.
Learn more about Controlled Not Gate as a joint reshuffling operator. If you feed in Basis States,A basis state in quantum computing is one of the fundamental states that form the building blocks of a quantum system’s state space. For a single qubit, the basis states are and ; any other qubit state is a superposition of these. In systems with multiple qubits, basis states are all possible combinations of s and s (e.g., , , , and ), forming an orthonormal basis for the system’s Hilbert space.
Learn more about Basis State you see a classical permutation. If you feed in Superpositions,Superposition in quantum computing means a quantum bit (qubit) can exist in multiple states (0 and 1) at the same time, rather than being limited to one like a classical bit. Mathematically, it’s a linear combination of basis states with complex probability amplitudes. This allows quantum computers to process many possible inputs simultaneously, enabling exponential speedups for certain problems.
Learn more about Superposition you get conditional correlations and often Entanglement.Entanglement is a quantum phenomenon where two or more particles become correlated so that measuring one instantly determines the state of the other, no matter how far apart they are. This correlation arises because their quantum states are linked as a single system, not as independent parts. It doesn’t allow faster-than-light communication but shows that quantum systems can share information in ways classical physics can’t explain.
Learn more about Entanglement That is its real power.

What Does The CNOT Operator Do?

From a simple swap of amplitudes to real effects you can measure

October 7, 2025•5 min

The CNOT operator does not create a cause-effect relationship. It does not even have a directed effect. It's only a simple swap of amplitudes. But one that produces Boolean logic, phase kickback, or entanglement, depending on how you look at it.