Tutorial

How To Make A Qubit Represent A Probability

Even though probabilities are not what you should care about

Ry-Gate is the direct way to control measurement probabilities. At least, it seems that way. But it is based on a fundamental assumption that, if not met, will break your code.

by Frank Zickert

December 11, 2025

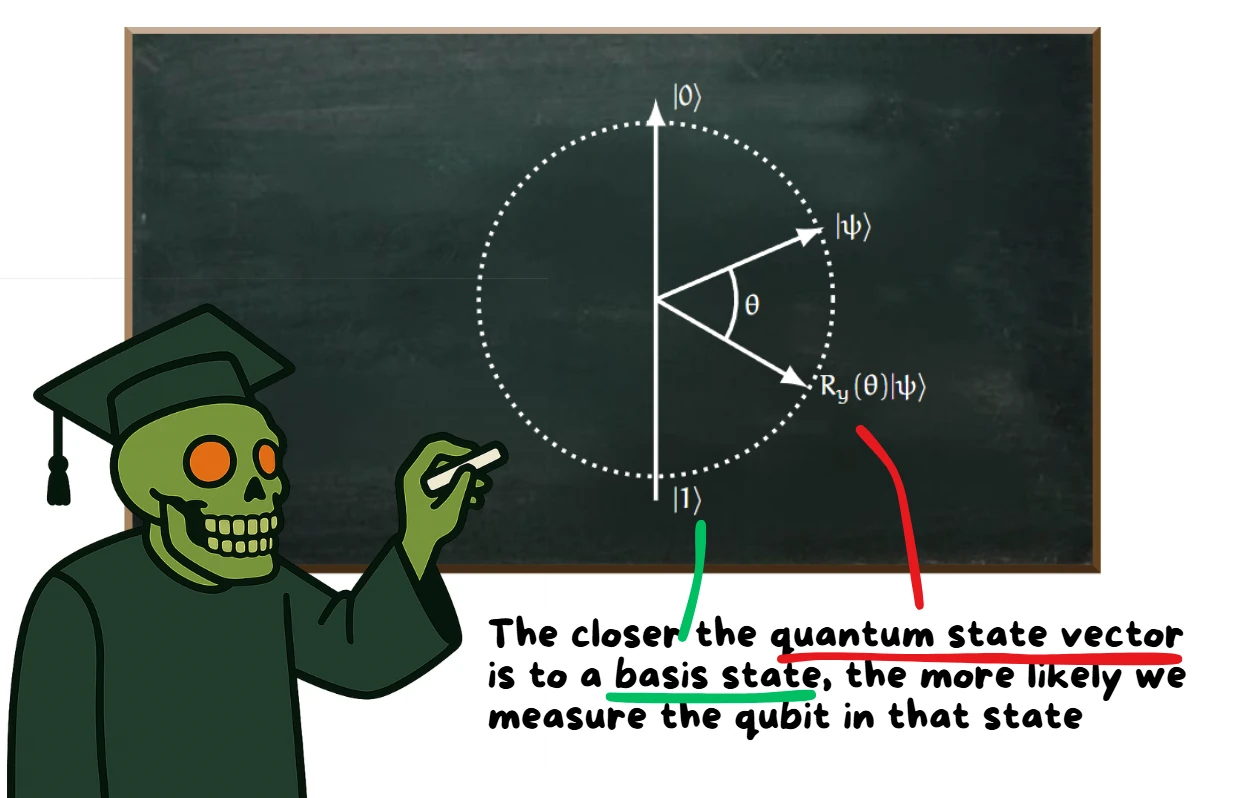
The Ry gate is a single-QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit Quantum GateA quantum gate is a basic operation that changes the state of one or more qubits, similar to how a logic gate operates on bits in classical computing. It uses unitary transformations, meaning it preserves the total probability (the state’s length in complex space). Quantum gates enable superposition and entanglement, allowing quantum computers to perform computations that classical ones cannot efficiently replicate.
Learn more about Quantum Gate that rotates a Qubit'sA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit state around the -axis of the Bloch sphere by a specified angle ("theta"). It changes the probabilities (through the AmplitudesIn quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude) of measuring is a basis state.
Learn more about or is a basis state.
Learn more about without altering their relative Quantum Phase.A **quantum phase** is the angle component of a particle’s wavefunction that determines how its probability amplitude interferes with others. It doesn’t affect observable probabilities directly but becomes crucial when comparing two or more states, as phase differences lead to interference effects. Essentially, it encodes the relative timing or “alignment” of quantum waves.
Learn more about Quantum Phase

The above image shows that effect in a two-dimensional representation that omits the complexA complex number is a number that has two parts: a real part and an imaginary part, written as , where . The real part behaves like ordinary numbers, while the imaginary part represents a direction perpendicular to the real axis on the complex plane. Complex numbers let us represent and calculate quantities involving square roots of negative numbers.
Learn more about Complex Number Quantum PhaseA **quantum phase** is the angle component of a particle’s wavefunction that determines how its probability amplitude interferes with others. It doesn’t affect observable probabilities directly but becomes crucial when comparing two or more states, as phase differences lead to interference effects. Essentially, it encodes the relative timing or “alignment” of quantum waves.
Learn more about Quantum Phase.

The closer the head of the Quantum State VectorA quantum state vector is a mathematical object (usually denoted |ψ⟩) that fully describes the state of a quantum system. Its components give the probability amplitudes for finding the system in each possible basis state. The squared magnitude of each component gives the probability of measuring that corresponding outcome.
Learn more about Quantum State Vector is to either Basis StateA basis state in quantum computing is one of the fundamental states that form the building blocks of a quantum system’s state space. For a single qubit, the basis states are and ; any other qubit state is a superposition of these. In systems with multiple qubits, basis states are all possible combinations of s and s (e.g., , , , and ), forming an orthonormal basis for the system’s Hilbert space.
Learn more about Basis State is a basis state.
Learn more about or is a basis state.
Learn more about the more likely we measureIn quantum computing, measurement is the process of extracting classical information from a quantum state. It collapses a qubit’s superposition into one of its basis states (usually or ), with probabilities determined by the amplitudes of those states. After measurement, the qubit’s state becomes definite, destroying the original superposition.
Learn more about Measurement the QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit in that state.

This post is accompanied by a PDF file summarizing the key points.

Please Login to Download the PDF (your PyQML subscription works here!)

Rotating the Quantum State VectorA quantum state vector is a mathematical object (usually denoted |ψ⟩) that fully describes the state of a quantum system. Its components give the probability amplitudes for finding the system in each possible basis state. The squared magnitude of each component gives the probability of measuring that corresponding outcome.
Learn more about Quantum State Vector around the y-axis (which would protrude perpendicularly from the center of the circle) therefore has a direct influence on the MeasurementIn quantum computing, measurement is the process of extracting classical information from a quantum state. It collapses a qubit’s superposition into one of its basis states (usually or ), with probabilities determined by the amplitudes of those states. After measurement, the qubit’s state becomes definite, destroying the original superposition.
Learn more about Measurement probabilities .

? shows how the Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate works in Qiskit.Qiskit is an open-source Python framework for programming and simulating quantum computers. It lets users create quantum circuits, run them on real quantum hardware or simulators, and analyze the results. Essentially, it bridges high-level quantum algorithms with low-level hardware execution.
Learn more about Qiskit

ry_gate.py

from math import pi

from qiskit import QuantumCircuit

from qiskit.quantum_info import Statevector

from qiskit.visualization import plot_histogram

# initialize a quantum circuit with a single qubit

qc = QuantumCircuit(1)

# the angles in radians to rotate the state vector

theta = pi / 3

# apply the roation angle to the qubit at position 0

qc.ry(theta, 0)

# turn quantum circuit into statevector

psi = Statevector.from_instruction(qc)

# show the data

print(f"|ψ⟩: {psi.data}")

# compute the probabilities from the statevector

# and show them in a histogram

plot_histogram(psi.probabilities_dict())

Listing 1 Using the Ry gate in Qiskit

In this code listing, we

the required functions from math and Qiskit,
a QuantumCircuit instance (qc) with a single Qubit.A qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit QiskitQiskit is an open-source Python framework for programming and simulating quantum computers. It lets users create quantum circuits, run them on real quantum hardware or simulators, and analyze the results. Essentially, it bridges high-level quantum algorithms with low-level hardware execution.
Learn more about Qiskit initializes QubitsA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit in the state ,
the angle theta in radians,
the Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate with the specified angle theta to the first (and only) QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit at position 0 of the qc,
the qc Quantum CircuitA quantum circuit is a sequence of quantum gates applied to qubits, representing the operations in a quantum computation. Each gate changes the qubits’ state using quantum mechanics principles like superposition and entanglement. The final qubit states, when measured, yield the circuit’s computational result probabilistically.
Learn more about Quantum Circuit into a Statevector class instance by using the static method from_instruction.

The Statevector class allows us to analyze the resulting Quantum State VectorA quantum state vector is a mathematical object (usually denoted |ψ⟩) that fully describes the state of a quantum system. Its components give the probability amplitudes for finding the system in each possible basis state. The squared magnitude of each component gives the probability of measuring that corresponding outcome.
Learn more about Quantum State Vector and reason about its implications, such as its raw data. That is the amplitudes depicted in ?.

|ψ⟩: [0.8660254+0.j 0.5 +0.j]

Listing 2 The resulting amplitudes of the Ry gate

We can also a histogram of the MeasurementIn quantum computing, measurement is the process of extracting classical information from a quantum state. It collapses a qubit’s superposition into one of its basis states (usually or ), with probabilities determined by the amplitudes of those states. After measurement, the qubit’s state becomes definite, destroying the original superposition.
Learn more about Measurement probabilities associated with this Quantum State VectorA quantum state vector is a mathematical object (usually denoted |ψ⟩) that fully describes the state of a quantum system. Its components give the probability amplitudes for finding the system in each possible basis state. The squared magnitude of each component gives the probability of measuring that corresponding outcome.
Learn more about Quantum State Vector resulting in ?.

Figure 1 Histogram of the probabilities resulting from the circuit

As we see, rotating the Quantum State VectorA quantum state vector is a mathematical object (usually denoted |ψ⟩) that fully describes the state of a quantum system. Its components give the probability amplitudes for finding the system in each possible basis state. The squared magnitude of each component gives the probability of measuring that corresponding outcome.
Learn more about Quantum State Vector by corresponds to a resulting probability of measuringIn quantum computing, measurement is the process of extracting classical information from a quantum state. It collapses a qubit’s superposition into one of its basis states (usually or ), with probabilities determined by the amplitudes of those states. After measurement, the qubit’s state becomes definite, destroying the original superposition.
Learn more about Measurement the QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit as is a basis state.
Learn more about of .

Apparently, since the Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate rotates the Quantum State VectorA quantum state vector is a mathematical object (usually denoted |ψ⟩) that fully describes the state of a quantum system. Its components give the probability amplitudes for finding the system in each possible basis state. The squared magnitude of each component gives the probability of measuring that corresponding outcome.
Learn more about Quantum State Vector around the -axis, we can directly control the resulting MeasurementIn quantum computing, measurement is the process of extracting classical information from a quantum state. It collapses a qubit’s superposition into one of its basis states (usually or ), with probabilities determined by the amplitudes of those states. After measurement, the qubit’s state becomes definite, destroying the original superposition.
Learn more about Measurement probabilities. So, if what we care about is probability, why not think directly in probabilities and let the angle take care of itself?

In fact, we don't even need to specify the angle ourselves. We can compute it classically.

Join to continue

This part is available to PyQML students and above. Log in or start a subscription to unlock member content.

Already a member? Use Log in. New here? Choose Subscribe.

Probabilities come from absolute squared Amplitudes.In quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude The Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate produces real AmplitudesIn quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude with a fixed sine cosine structure. That structure can be inverted exactly. If you want a probability p of measuringIn quantum computing, measurement is the process of extracting classical information from a quantum state. It collapses a qubit’s superposition into one of its basis states (usually or ), with probabilities determined by the amplitudes of those states. After measurement, the qubit’s state becomes definite, destroying the original superposition.
Learn more about Measurement is a basis state.
Learn more about , you solve

which gives

That single equation turns probability into geometry.

? adds a helper function prob_to_angle that a given real probability value into an equivalent rotation angle.

ry_gate.py

from math import asin, pi, sqrt

from qiskit import QuantumCircuit

from qiskit.quantum_info import Statevector

from qiskit.visualization import plot_histogram

def prob_to_angle(prob: float) -> float:

    # Converts a given real probability value into an equivalent rotation angle.

    return 2 * asin(sqrt(prob))

# initialize a quantum circuit with a single qubit

qc = QuantumCircuit(1)

# apply the roation angle that corresponds to the

# specified probability

qc.ry(prob_to_angle(0.6), 0)

# turn quantum circuit into statevector

psi = Statevector.from_instruction(qc)

# compute the probabilities from the statevector

# and show them in a histogram

plot_histogram(psi.probabilities_dict())

Listing 3 The prob-to-angle helper function

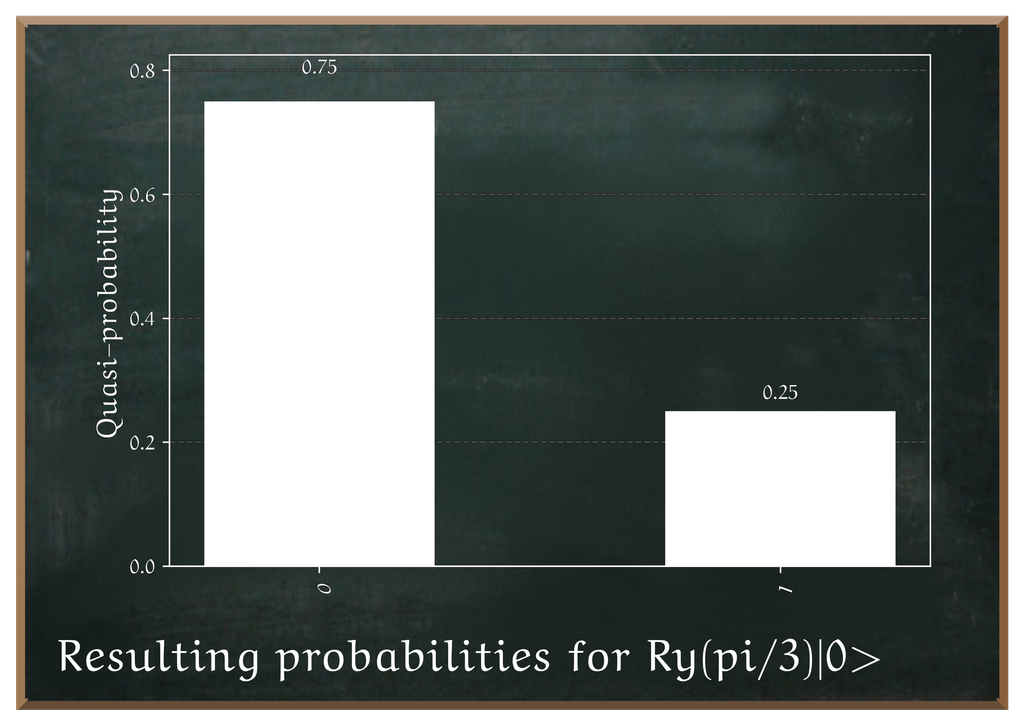
We use the prob_to_angle function to calculate the angle we into the Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate. The result is a Quantum State VectorA quantum state vector is a mathematical object (usually denoted |ψ⟩) that fully describes the state of a quantum system. Its components give the probability amplitudes for finding the system in each possible basis state. The squared magnitude of each component gives the probability of measuring that corresponding outcome.
Learn more about Quantum State Vector whose MeasurementIn quantum computing, measurement is the process of extracting classical information from a quantum state. It collapses a qubit’s superposition into one of its basis states (usually or ), with probabilities determined by the amplitudes of those states. After measurement, the qubit’s state becomes definite, destroying the original superposition.
Learn more about Measurement probability for corresponds to the specified value of 0.6 as the histogram in ? denotes.

Figure 2 Histogram of the probabilities resulting from the circuit

Once you have a function that converts probability into an angle, it is tempting to reuse it. If it worked once, it should work again.

However, this calculation of only works under the assumption that the QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit starts in the state is a basis state.
Learn more about . If the initial Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State is different, the relationship between the angle and probability changes.

That assumption is where things break. You apply one rotation to encode a probability. Then you apply another rotation, computed the same way, to change it. The result is wrong. The histogram jumps somewhere unexpected. It feels like the QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit ignored your instruction. The formula is not wrong. The mental model is. The Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate does not overwrite probabilities. It adds angles.

? shows what happens when we add another Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate.

ry_gate.py

# initialize a quantum circuit with a single qubit

qc = QuantumCircuit(1)

# apply the roation angle that corresponds to the

# specified probability

qc.ry(prob_to_angle(0.6), 0)

# apply the rotation on a vector that is not in state |0⟩

qc.ry(prob_to_angle(0.2), 0)

# turn quantum circuit into statevector

psi = Statevector.from_instruction(qc)

# compute the probabilities from the statevector

# and show them in a histogram

plot_histogram(psi.probabilities_dict())

Listing 4 Applying an Ry gate on a different state than |0>

The Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate rotates the Quantum State VectorA quantum state vector is a mathematical object (usually denoted |ψ⟩) that fully describes the state of a quantum system. Its components give the probability amplitudes for finding the system in each possible basis state. The squared magnitude of each component gives the probability of measuring that corresponding outcome.
Learn more about Quantum State Vector such that it corresponds to a probability of 0.6 computed by prob_to_angle(0.6).

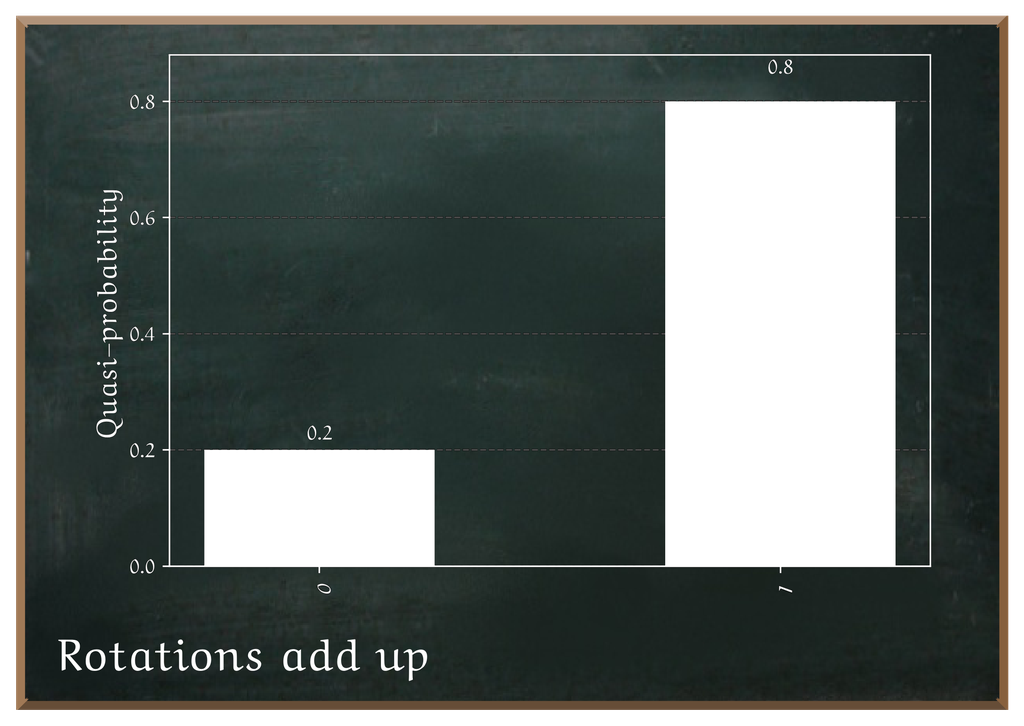
Accordingly, we could assume that a rotation of prob_to_angle(0.2) would result in an overall probability of measuring of .

This is not the case, though, as ? indicates.

Figure 3 Result of two rotations

We end up with a probability of of measuring the QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit in .

The reason for this is that the second rotation does not act on a QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit in the state . It acts on the state that has already been transformed by the first rotation. However, the function prob_to_angle(p) only works as intended if the input state is exactly , since the underlying formula is based on the identity

which gives a direct and simple link between the angle acting on state and the resulting probability of measuring .

Yet, after the first rotation, the QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is no longer in . It is in a superposition with nonzero amplitudes for both and . When you apply the second rotation, the Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate mixes these existing amplitudes according to its matrix rule, rather than adding the probabilities linearly.

The call to prob_to_angle(0.2) cannot therefore be interpreted as add to the probability of the result . Instead, it rotates the already tilted Quantum State VectorA quantum state vector is a mathematical object (usually denoted |ψ⟩) that fully describes the state of a quantum system. Its components give the probability amplitudes for finding the system in each possible basis state. The squared magnitude of each component gives the probability of measuring that corresponding outcome.
Learn more about Quantum State Vector again, changing the geometry of the state in a nonlinear way. This geometric complication is the reason why the final probability is approximately instead of the expected .

In short, each Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate acts on the current AmplitudeIn quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude structure and not on your desired probability target. For this reason, successive rotations can lead to results that appear unexpectedly large from a purely probabilistic point of view.

At this point the QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is no longer a probability container. It is a point on a sphere with memory. Geometry remembers history. Probability does not. What sounds like a limitation is actually a clue. Every probability corresponds to a unique angle. The current Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State already has an angle, whether you tracked it or not. Moving from one probability to another is simply moving from one angle to another.

We must include the current AmplitudesIn quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude of the Quantum State VectorA quantum state vector is a mathematical object (usually denoted |ψ⟩) that fully describes the state of a quantum system. Its components give the probability amplitudes for finding the system in each possible basis state. The squared magnitude of each component gives the probability of measuring that corresponding outcome.
Learn more about Quantum State Vector in the function that calculates , as shown in ?, where the calculation explicitly takes into account the current state of the QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit before determining the rotation required to achieve the desired final probability.

ry_gate.py

def prob_to_angle_from_old_prob(old_prob: float, target_prob: float) -> float:

"""

    Compute the angle theta that corresponds to a target

    prob given the qubit state vector has already been rotated

"""

    return prob_to_angle(target_prob) - prob_to_angle(old_prob)

# initialize a quantum circuit with a single qubit

qc = QuantumCircuit(1)

# apply the roation angle that corresponds to the

# specified probability

qc.ry(prob_to_angle(0.6), 0)

# apply the rotation on a vector that is not in state |0⟩

qc.ry(prob_to_angle_from_old_prob(0.6, 0.8), 0)

# turn quantum circuit into statevector

psi = Statevector.from_instruction(qc)

# compute the probabilities from the statevector

# and show them in a histogram

plot_histogram(psi.probabilities_dict())

Listing 5 prob_to_angle taking into account the previous probability

The function prob_to_angle_from_old_prob two probabilities as parameters. It assumes that the qubit has already been rotated away from the Basis StateA basis state in quantum computing is one of the fundamental states that form the building blocks of a quantum system’s state space. For a single qubit, the basis states are and ; any other qubit state is a superposition of these. In systems with multiple qubits, basis states are all possible combinations of s and s (e.g., , , , and ), forming an orthonormal basis for the system’s Hilbert space.
Learn more about Basis State .

That means the QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit is in state .

Since Ry GatesThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate add their rotation angles when applied in sequence, the total rotation after applying a second Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate will be

The MeasurementIn quantum computing, measurement is the process of extracting classical information from a quantum state. It collapses a qubit’s superposition into one of its basis states (usually or ), with probabilities determined by the amplitudes of those states. After measurement, the qubit’s state becomes definite, destroying the original superposition.
Learn more about Measurement probability for outcome depends only on this total angle, through the identity:

So, to apply a rotation angle that corresponds to the target_prob, we must subtract the angle that corresponds to the old_prob.

The function implements this idea directly. It the old probability and subtracts it from the target probability. In other terms, the function undoes the first rotation and applies the new. In one single Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate.

? shows the resulting probabilities. It leaves the QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit in a Quantum StateA quantum state is the complete mathematical description of a quantum system, containing all the information needed to predict measurement outcomes. It’s usually represented by a wavefunction or a state vector in a Hilbert space. The state defines probabilities, not certainties, for observable quantities like position, momentum, or spin.
Learn more about Quantum State whose AmplitudesIn quantum computing an amplitude is a complex number that describes the weight of a basis state in a quantum superposition. The squared magnitude of an amplitude gives the probability of measuring that basis state. Amplitudes can interfere, this means adding or canceling, allowing quantum algorithms to bias outcomes toward correct solutions.
Learn more about Amplitude correspond to the specified probability.

Figure 4 Computing the angles correctly

This looks like bookkeeping, and it is. But that bookkeeping restores predictability. You are no longer fighting the QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit. You are working with its geometry.

In Quantum ComputingQuantum Computing is a different kind of computation that builds upon the phenomena of Quantum Mechanics.
Learn more about Quantum Computing probabilities are everywhere. Yet, you must remember that you don't work with probabilities directly. Instead, you work with rotation angles.

Rotations accumulate cleanly and reversibly. Probabilities enter only at Measurement.In quantum computing, measurement is the process of extracting classical information from a quantum state. It collapses a qubit’s superposition into one of its basis states (usually or ), with probabilities determined by the amplitudes of those states. After measurement, the qubit’s state becomes definite, destroying the original superposition.
Learn more about Measurement A QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit does not store probabilities or uncertainty. It stores the Quantum State Vector.A quantum state vector is a mathematical object (usually denoted |ψ⟩) that fully describes the state of a quantum system. Its components give the probability amplitudes for finding the system in each possible basis state. The squared magnitude of each component gives the probability of measuring that corresponding outcome.
Learn more about Quantum State Vector Probability is not written into the Qubit.A qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit It emerges when you look at it. Once you accept that probability is geometry, not noise, the Ry GateThe Ry gate is a single-qubit quantum gate that rotates a qubit’s state around the Y-axis of the Bloch sphere by a specified angle . It changes the probabilities (amplitudes) of measuring or without altering their relative phase.
Learn more about Ry Gate stops being a trick. It becomes a language for saying exactly what you want the QubitA qubit is the basic unit of quantum information, representing a superposition of 0 and 1 states.
Learn more about Quantum Bit to mean.